Building a Block Blast Solver 
Table of Contents
Introduction
This project started with a simple obsession—Block Blast. The satisfaction of beating my friends’ high scores while we were in a friendly competition to see who could get the highest score got me thinking about whether I could build a solver that could give me the best possible moves.
Block Blast is a Tetris inspired puzzle game where you drag and drop the pieces onto an 8x8 board and can clear both rows (like in Tetris) and columns; the pieces don't fall, you are presented with three at a time and drag them onto the board. You lose in a fashion similar to Tetris -- when there is no longer room to place a piece. The game's simplicity is its charm, but don't be fooled—mastering Block Blast takes skill, strategy, and a sharp mind.
I wanted a program that could analyze a screenshot when I was stuck and suggest the best moves. I decided to stay away from using AI as that seemed to defeat the challenge of the project.
Challenges Faced
The development process came with several interesting challenges:
| Challenge | Description |
|---|---|
| Game State Recognition | Unlike Tetris, Block Blast does not have a defined set of shapes. Capturing and understanding the game state accurately, including different block colors and patterns. |
| Game Logic | Block Blast has a unique game logic that requires a custom approach to solving the game. |
| Performance Optimization | Finding the right balance between speed and accuracy while managing computational resources. |
Game State Recognition
The first challenge was to capture the game state accurately. This was challenging because the game does not use a defined set of shapes or colors. I tried a few approaches:
Goal
Finding a simple solution to convert the uploaded image of the game board and the blocks within it to a 2D array of 0s and 1s respectively.
Approach 1: Simple Image Processing
My initial approach followed classic computer vision techniques:
- Crop image into 2 parts: the game board and the game pieces
- Convert image to grayscale
- Crop image to isolate the region of interest
- Apply binary thresholding to convert grayscale to black and white
- Resize binary image to a smaller grid (e.g., 8x8)
- Convert resized image to a NumPy array where any pixel value of 255 is converted to 1
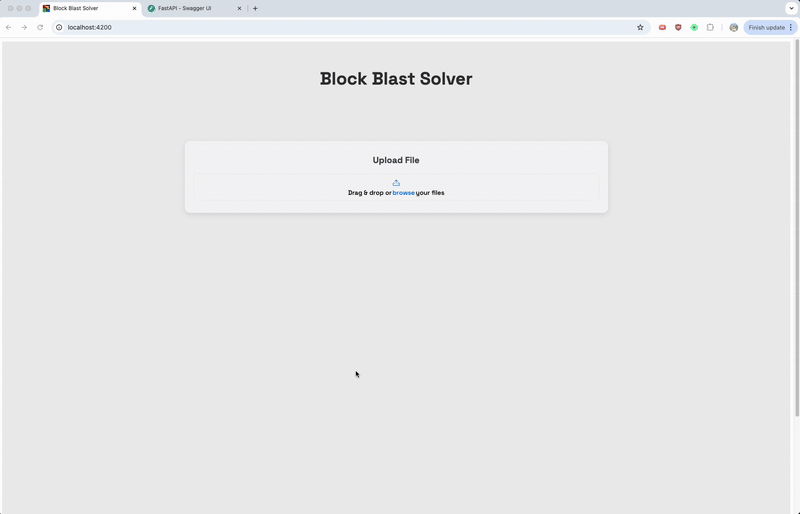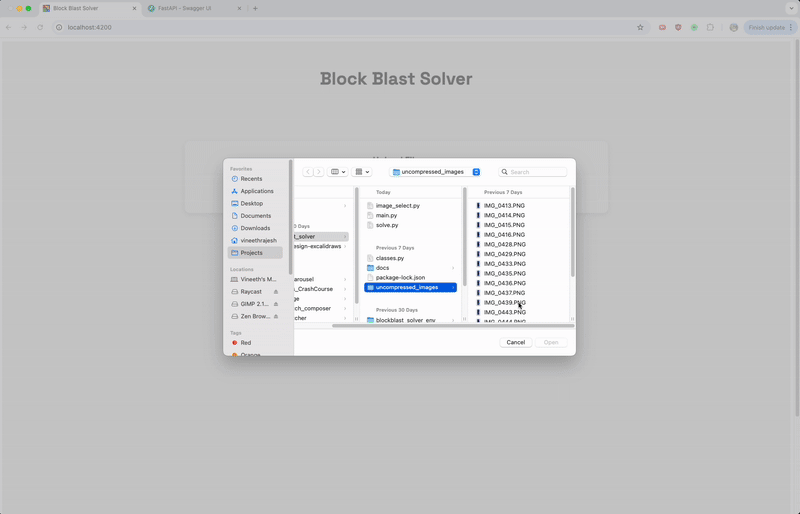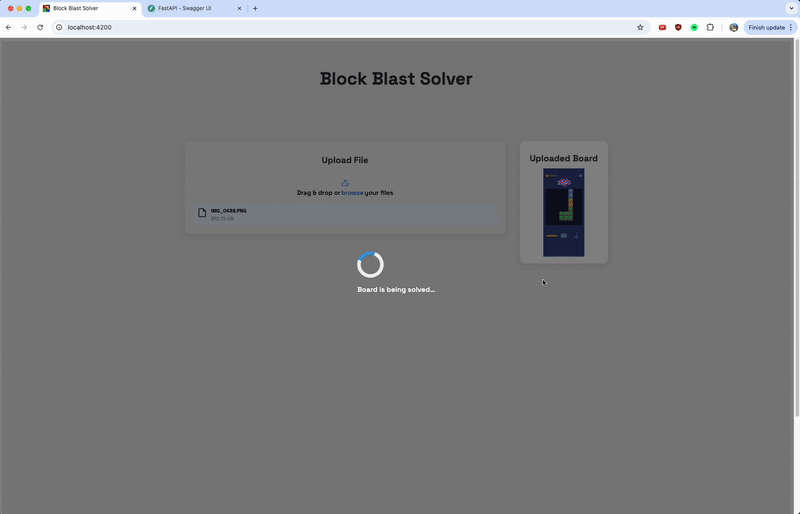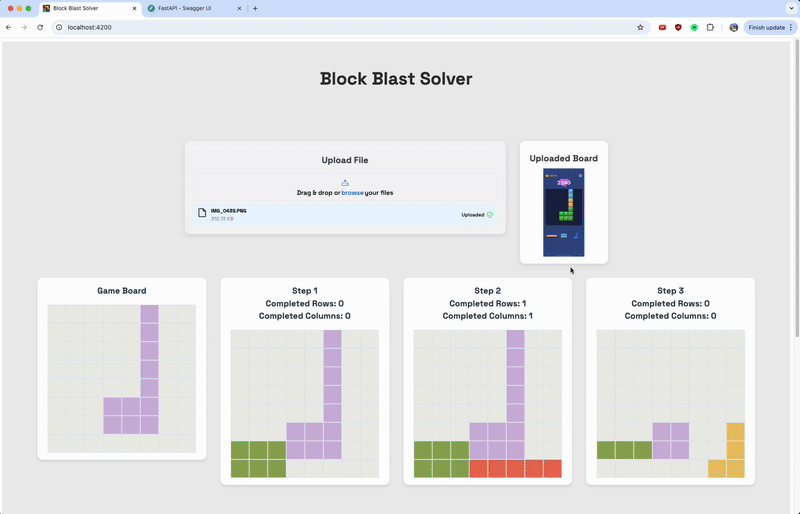
Visual demonstration of the process:

Step 1: Original Screenshot

Step 2: Grayscale

Step 3: Binary
[[1 1 1 0 0 0 0 1] [0 0 0 0 0 0 0 1] [0 0 0 0 0 0 0 1] [0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0] [0 1 1 0 0 0 0 0] [0 1 1 0 0 0 0 0]]
Final Matrix
Approach Evolution
Why the first method failed for game pieces:
- The results were inaccurate as shapes cannot be predefined as they are randomly generated.
- Background color interference made simple image processing unreliable
- Inconsistent results as shapes can be different shades of blue and because the background color is a shade of blue, it was difficult to do simple image processing and get a consistent binary image.
Approach 2: Using HSV Ranges
Attempted using HSV ranges to extract the shapes from the cropped images:
- This didn’t work because I suspect that some of the colors used are randomly generated or the number of colors was too large to manually identify.
- So hard coding the HSV color values wouldn’t work consistently.
Final Approach: Color Detection
After trying several methods that didn’t work consistently, I developed a color detection system that proved more reliable.
This proved to be quite challenging because it was tricky to get consistent results. It was easy to find the shape, but accurately obtaining the correct number of blocks of the shape was extremely inconsistent due to factors like image quality and resolution. I applied a number of techniques to improve the accuracy of the detection.
My color detection system consisted of 3 main steps:
Grid-Based Scanning
- The game board is divided into a grid where each cell represents a potential block position.
- Each cell is scanned systematically using a fixed block size (58 pixels) and small offset (10 pixels).
- This creates a consistent sampling pattern regardless of the board’s current state.
Multi-Point Sampling Strategy
- Instead of relying on a single pixel, each grid cell is sampled at 11 points.
- This multi-sample approach helps handle color variations and potential image noise.
Color Matching Algorithm
For each sampled point:
- Compare the pixel’s RGB values against a reference background color (48, 74, 139)
- Count both background matches and block (non-background) matches
- Calculate a ratio of block pixels to total valid samples
- Consider a cell to contain a block if more than 40% of samples are non-background
After the grid is scanned, the results are represented as a 2D array of 0s and 1s where 1s represent blocks and 0s represent background.
[[1 1 1 0 0 0 0 1] [0 0 0 0 0 0 0 1] [0 0 0 0 0 0 0 1] [0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0] [0 0 0 0 0 0 0 0] [0 1 1 0 0 0 0 0] [0 1 1 0 0 0 0 0]]
Board State
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 1. 1. 1. 1. 0. 0. 1. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
Pieces Detected
Approach to Game Logic
Now that we have detected the game board and the game pieces, we can start to think about the game logic.
Goal
Suggest the best possible moves given the current game state.
Does the game make us lose on purpose?
While developing the solver, I stumbled upon an interesting pattern. In the early game, the pieces you receive are suspiciously perfect for creating complete rows or columns, which suggests the game is aware of the pieces we need. At the start of the game at least, it helps us.
Solution Evolution
The solver uses:
- 2D array structure to represent the game state for fast operations
- Optimized pattern matching for move evaluation
The final strategy I developed is a combination of brute force and a scoring system that would reward moves based on piece position. The best position for each piece that will yield the highest score, we go through all possible positions for all pieces in all possible orders. Piece 1, then 2, then 3, then 1, then 3, then 2, etc. This is therefore a brute-force method, which takes a lot of time, especially when there are few pieces already placed on the board. The game rewards a player for completing rows and columns, so we want to maximize the number of rows and columns completed so I added an extra bonus to the score to emphasize this in the algorithm. I also penalize the creation of isolated blocks, meaning that if a move results in a single block surrounded by empty spaces at the end of a turn, it is penalized.
So my solution has 3 key components:
- Exhaustive Search: Examines all valid permutations of piece placements
- Tests every possible order of the three available pieces
- Considers all valid positions for each piece
- Computationally expensive but guarantees finding the optimal solution
- Strategic Scoring: Evaluates board states using weighted factors
- Primary reward: Completed rows/columns (+50 points)
- Secondary rewards: Adjacent pieces, border placements
- Penalties: Isolated blocks, trapped spaces
- Performance Optimizations:
- Early pruning of equivalent states in the early game
- Skip evaluation of clearly suboptimal positions
Scoring Methodology
| Factor | Impact |
|---|---|
| Neighbors | Increase score plus for each neighbor |
| Border placement | Increase score plus for each border placement |
| Completed rows/columns | Reward a bonus of 50 points |
| Isolated blocks | Score penalty |
| Holes | Score penalty |
The brute-force method can take a long time if the board is relatively empty. So, I added the below optimization:
- If the game state has a board with less than 15 squares filled, I skip boards (valid placements) with the same score, as doing it earlier would take too much time and also has no real value when there are no pieces yet.
Over Optimization: Something I ran into when trying to optimize the scoring methodology was increasing the score for partially completed rows/columns. This led to over-rewarding boards that have many filled cells even when they are not close to becoming complete. This can mislead the solver into choosing moves that rack up a lot of temporary points without actually progressing toward clearing rows/columns.
Final Thoughts
What started as a simple desire to beat my friend’s high scores turned into a fun journey through image processing, game theory, and optimization. I learnt a few lessons while developing this.
First, the obvious solution isn’t always the best one. My initial attempts with basic image processing seemed logical but failed spectacularly in practice. The path to a robust solution required stepping back, understanding the core challenges, and being willing to throw away code that I had invested time in.
The final solution, while not perfect, consistently suggests the best possible moves for the current game state. Building it helped me gave me an appreciation for the subtle complexities that lie beneath seemingly simple games.
Future Improvements
- Enhanced pattern recognition
- Special piece handling
- Caching of Board States
- Improved Scoring Methodology